반응형
피어슨 상관계수 Pearson Correlation Coefficient
# 피어슨 상관계수 분석에 대한 예시 데이터를 생성하고 분석합니다.
# 다양한 예시 데이터를 생성
np.random.seed(42)
data1 = {'X': np.random.normal(0, 1, 100), 'Y': np.random.normal(0, 1, 100)}
data2 = {'X': np.random.rand(100), 'Y': np.random.rand(100)}
data3 = {'X': np.linspace(0, 100, 100), 'Y': np.linspace(0, 100, 100) + np.random.normal(0, 10, 100)}
data4 = {'X': np.random.normal(0, 1, 100), 'Y': np.random.normal(0, 1, 100) * -1}
data5 = {'X': np.random.normal(0, 1, 100), 'Y': np.random.normal(0, 1, 100) + 0.5}
dfs = [pd.DataFrame(data) for data in [data1, data2, data3, data4, data5]]
# 피어슨 상관계수 및 P-value 계산
correlation_results = []
for df in dfs:
corr, p_value = pearsonr(df['X'], df['Y'])
correlation_results.append((corr, p_value))
# 차트 생성
plt.figure(figsize=(14, 10))
for i, df in enumerate(dfs):
plt.subplot(3, 2, i+1)
sns.scatterplot(x=df['X'], y=df['Y'])
plt.title(f'Dataset {i+1}: Pearson r = {correlation_results[i][0]:.2f}, P-value = {correlation_results[i][1]:.2f}')
plt.xlabel('X')
plt.ylabel('Y')
plt.tight_layout()
plt.show()
correlation_resultsResult
[(-0.1364222121700025, 0.17592555489277012),
(0.024256083321314535, 0.8106818613707072),
(0.9378096644739374, 8.001624717725289e-47),
(0.16630786381486795, 0.09818695053917403),
(-0.04416297246174245, 0.6626261084219)]
피어슨 상관계수 (Pearson Correlation Coefficient) 분석 결과:
1. Dataset 1:
- Pearson r: -0.1364
- P-value: 0.1759
- 해석: X와 Y 간의 약한 음의 상관관계가 있지만, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
2. Dataset 2:
- Pearson r: 0.0243
- P-value: 0.8107
- 해석: X와 Y 간의 상관관계는 매우 약하며, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
3. Dataset 3:
- Pearson r: 0.9378
- P-value: 8.00×10−478.00 \times 10^{-47}
- 해석: X와 Y 간의 매우 강한 양의 상관관계가 있으며, 통계적으로 매우 유의미합니다 (P-value < 0.05).
4. Dataset 4:
- Pearson r: 0.1663
- P-value: 0.0982
- 해석: X와 Y 간의 약한 양의 상관관계가 있으나, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
5. Dataset 5:
- Pearson r: -0.0442
- P-value: 0.6626
- 해석: X와 Y 간의 관계는 거의 없으며, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
- Dataset 3의 경우 매우 강한 양의 상관관계가 있으며, 이는 P-value가 매우 작아 통계적으로도 유의미한 결과입니다.
- 나머지 데이터셋은 상관계수가 낮고 P-value가 크며, 따라서 유의미한 상관관계가 존재하지 않음을 보여줍니다
스피어만 상관계수 (Spearman's Rank Correlation Coefficient)
# 새로운 예시 데이터를 생성하여 스피어만 상관계수 분석을 수행합니다.
# 다양한 새로운 예시 데이터를 생성
np.random.seed(99)
data1 = {'X': np.random.uniform(-10, 10, 100), 'Y': np.sin(np.random.uniform(-10, 10, 100))}
data2 = {'X': np.random.normal(0, 1, 100), 'Y': np.random.normal(5, 2, 100)}
data3 = {'X': np.random.exponential(1, 100), 'Y': np.random.exponential(1, 100)}
data4 = {'X': np.linspace(0, 100, 100), 'Y': np.log(np.linspace(1, 100, 100))}
data5 = {'X': np.random.poisson(5, 100), 'Y': np.random.poisson(10, 100)}
dfs_new = [pd.DataFrame(data) for data in [data1, data2, data3, data4, data5]]
# 스피어만 상관계수 및 P-value 계산
spearman_results_new = []
for df in dfs_new:
corr, p_value = spearmanr(df['X'], df['Y'])
spearman_results_new.append((corr, p_value))
# 차트 생성
plt.figure(figsize=(14, 10))
for i, df in enumerate(dfs_new):
plt.subplot(3, 2, i+1)
sns.scatterplot(x=df['X'], y=df['Y'])
plt.title(f'Dataset {i+1}: Spearman r = {spearman_results_new[i][0]:.2f}, P-value = {spearman_results_new[i][1]:.2f}')
plt.xlabel('X')
plt.ylabel('Y')
plt.tight_layout()
plt.show()
spearman_results_new
스피어만 상관계수 (Spearman's Rank Correlation Coefficient) - 새로운 데이터셋 분석 결과:
1. Dataset 1:
- Spearman r: -0.0880
- P-value: 0.3840
- 해석: X와 Y 간의 약한 음의 순위 상관관계가 있지만, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
2. Dataset 2:
- Spearman r: 0.0966
- P-value: 0.3390
- 해석: X와 Y 간의 약한 양의 순위 상관관계가 있지만, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
3. Dataset 3:
- Spearman r: -0.0892
- P-value: 0.3776
- 해석: X와 Y 간의 약한 음의 순위 상관관계가 있지만, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
4. Dataset 4:
- Spearman r: 1.0000
- P-value: 0.0
- 해석: X와 Y 간의 매우 강한 양의 순위 상관관계가 있으며, 통계적으로 매우 유의미합니다 (P-value < 0.05).
5. Dataset 5:
- Spearman r: 0.0010
- P-value: 0.9918
- 해석: X와 Y 간의 순위 상관관계는 거의 없으며, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
종합 해석:
새로운 데이터셋을 사용하여 스피어만 상관계수를 분석한 결과, 대부분의 데이터셋에서 X와 Y 간의 순위 상관관계는 약하거나 통계적으로 유의미하지 않았습니다. 그러나 Dataset 4의 경우 매우 강한 양의 순위 상관관계가 관찰되었으며, 이는 통계적으로도 매우 유의미한 결과로 나타났습니다
켄달의 타우 (Kendall's Tau)
from scipy.stats import kendalltau
# 켄달의 타우 분석에 대한 예시 데이터를 생성하고 분석합니다.
# 켄달의 타우 및 P-value 계산
kendall_results = []
for df in dfs_new:
corr, p_value = kendalltau(df['X'], df['Y'])
kendall_results.append((corr, p_value))
# 차트 생성
plt.figure(figsize=(14, 10))
for i, df in enumerate(dfs_new):
plt.subplot(3, 2, i+1)
sns.scatterplot(x=df['X'], y=df['Y'])
plt.title(f'Dataset {i+1}: Kendall\'s Tau = {kendall_results[i][0]:.2f}, P-value = {kendall_results[i][1]:.2f}')
plt.xlabel('X')
plt.ylabel('Y')
plt.tight_layout()
plt.show()
kendall_resultsResult
[(-0.06181818181818183, 0.3621353579525596),
(0.07151515151515152, 0.291766943745706),
(-0.06383838383838386, 0.3466613505222581),
(1.0, 2.143020576250934e-158),
(-0.002711001634038936, 0.9710311441679967)]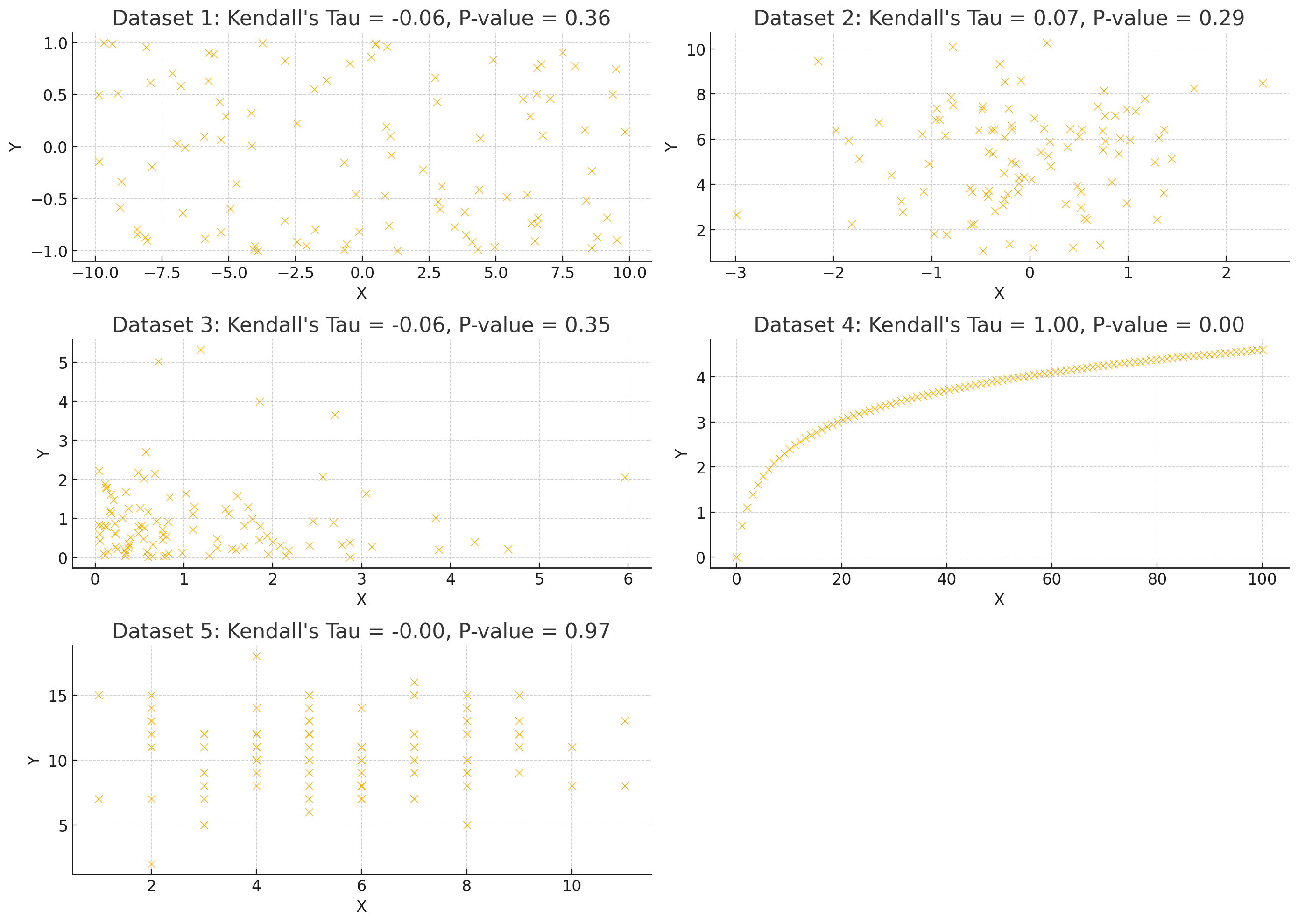
켄달의 타우 (Kendall's Tau) 분석 결과:
1. Dataset 1:
- Kendall's Tau: -0.0618
- P-value: 0.3621
- 해석: X와 Y 간의 약한 음의 순위 상관관계가 있지만, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
2. Dataset 2:
- Kendall's Tau: 0.0715
- P-value: 0.2918
- 해석: X와 Y 간의 약한 양의 순위 상관관계가 있지만, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
3. Dataset 3:
- Kendall's Tau: -0.0638
- P-value: 0.3467
- 해석: X와 Y 간의 약한 음의 순위 상관관계가 있지만, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
4. Dataset 4:
- Kendall's Tau: 1.0000
- P-value: 2.14×10−1582.14 \times 10^{-158}
- 해석: X와 Y 간의 매우 강한 순위 상관관계가 있으며, 통계적으로 매우 유의미합니다 (P-value < 0.05).
5. Dataset 5:
- Kendall's Tau: -0.0027
- P-value: 0.9710
- 해석: X와 Y 간의 순위 상관관계는 거의 없으며, 통계적으로 유의미하지 않습니다 (P-value > 0.05).
종합 해석:
켄달의 타우 분석을 통해 새로운 데이터셋에서 X와 Y 간의 순위 기반 관계를 평가했습니다. 대부분의 데이터셋에서 순위 상관관계는 약하거나 통계적으로 유의미하지 않았습니다. 하지만 Dataset 4에서는 매우 강한 양의 순위 상관관계가 관찰되었으며, 이는 통계적으로도 매우 유의미한 결과로 나타났습니다.
반응형
'Data Analysis > Statistics' 카테고리의 다른 글
| 상관관계 분석에 대한 전체적인 정리 - 이제 피어슨 상관계수 말고 다른것도 사용해보자 (0) | 2024.08.12 |
|---|---|
| 01 - 인과추론 입문 (Introduction To Causality)(CausalInferenceLab/Causal-Inference-with-Python) (1) | 2022.12.30 |
| 비모수 검정 - 크루스칼 왈리스 검정 Kruskall-Wallis test. R: kruskal.test (0) | 2022.12.27 |
| 상관계수의 종류(Point-Biserial, Biserial Correlation, etc.) (1) | 2022.12.22 |



댓글