상관계수의 종류(Point-Biserial, Biserial Correlation, etc.)

 

상관계수의 종류(Point-Biserial, Biserial Correlation, etc.)

 

 

Pearson r: 피어슨 상관계수 

• x: 연속형 y : 연속형일때 사용 / 두개의 수치값들의 집합이 있을 때
• 즉 , 두 수치값들이 서로 관련이 있냐 ? 라고 물어보면 대답할때 사용한다.
  • 우리반 학생들 수학도 잘하고 영어도 잘하는게 상관이 있냐 ?  혹은 수학이랑 물리랑 상관이 있냐 ? 이러한 질문에 답할때 사용한다.
  • 두 변수의 결합은 정규분포일 것이라는 가정이 포함
    • 엄밀하게  피어슨 상관계수는 두 변수가 정규분포여야 한다는 전제를 두지는 않지만 피어슨 상관계수는 정규분포에서 가장 잘 작동하도록 설계되었다
  • 그러므로 이상치에 매우 민감하다 
    • 편차의 곱들이 정규분포를 따르지 않으면 오해석을 만드는 이상치(outlier)에 예민한 문제가 있다.
  • 인과관계와 관련이 있을 것이라는 해석을 하게 되면 큰일난다.... 
    • 인과 관계 증명이 필요하면 regression test를 수행해야 한다.
    • 횡단면 데이터(cross-sectional) 또는 시계열 데이터(time-series)에 대해서 모두 사용할 수 있지만 시계열 데이터에는 해석을 매우 주의해야 하거나 사용하지 않아야 한다.

공식 : 

공분산을 각각의 분산으로 나눈다는 것일 뿐

- 표준편차 곱한값을 분모로 공분산을 분자로 둔다. 

자기 자신과의 공분산은 분산이기 때문에 1이 나온다. 

 

왜 ? 

• -  서로 같이 변화하는 정도를 어떤 식으로 수치화할 수 있는가?? 
  • 두 확률변수 x y 가 각각의 평균 mean() 에 대해서 얼마나 같이 흩어져(떨어져) 있는지를 구하기 - 분산이나 표준 편차의 개념 
  • 서로 곱해 합한 후에 평균 내어 수치화하면 대충 맞지 않을까 하는 접근
  • 각 x, y 쌍 데이터의 각 평균으로부터의 차이에 대한 면적을 계산하는 개념 
  •  (x−¯x)(y−y¯)의 부호 4 사분면으로 따져보면 공분산이 Positive = + r 가 훨씬 많음 / 공분산이 Negative = - 가 훨씬 많음 / +와 -값이 비등하게 있다면 = 다 더하면 0에 가까움  

 

문제는 ?

• 값의 크기 보다는 Sign(부호)에 의해서 선형 관계의 방향을 나타냄 
• 1000점 만점의 영어성적과 수학성적의 공분산과 50점 만점의 영어성적과 수학 성적을 비교하게 되면 1000점 만점의 영어성적과 수학 성적의 상관관계가 더 적더라도 50점 만점의 공분산이 더 큰 값을 가질 수 있음
• 이 단점을 해결하기 위해서 = 정규화 (각각의 표준편차로 정규화를 한다는 것)
  • 선형 관계의 Strength도 다른 것과 비교해서 알 수 있고, 방향도 알 수 있는 그런 지표가 됨

 

https://recipesds.tistory.com/entry/Covariance-%EA%B3%B5%EB%B6%84%EC%82%B0%EA%B3%BC-Pearson-%EC%83%81%EA%B4%80%EA%B3%84%EC%88%98%EC%9D%98-%EC%86%8D%EC%82%AC%EC%A0%95

Covariance 공분산과 Pearson 상관계수의 속사정. 그리고 Spearman의 꼽사리

공분산(Covariance)

• - 기존의 표본에 대한 분산을 두 변수에 적용하여 계산한 것이 공분산
  • 공분산은 2개의 확률변수의 차이에 대한 분산이 아닌 같이 변화하는 양을 나타내는 상관 정도를 나타내는 값
  • 분산은 값이 클수록 더 흩어지는데 공분산은 값이클수록 더 흩어지지 않는다. 
• - 공분산은 Covariance를 그대로 한국어로 번역했는데 이건 전혀 이해에 도움이 되지 않는 해석

- 추가 학습 목록 :

• Cook’s distance: outlier 무력화
• Bootstrapping: 편추정에 대한 방지

 상관계수의 검정 

• 회귀 계수로 가능함
• 상관계수가 어떤 분포를 따를지를 알아야 Null Hypothesis를 세울 수 있겠는데 (모집단의 분산을 σ²으로, 표본의 분산을 s²로 표시하듯이 모집단의 상관계수를 ρ로 표본의 상관계수를  r로 표현)
•  

 

 

 

---

Spearman 상관계수

• Spearman's r.

• – 서열척도들간의 상관계수상관관계를 볼 때 Outlier가 있거나 비선형관계일 때는 상관계수가 의미를 퇴색합니다. 당연하겠지만 비선형관계일 때는 의미를 찾기 어렵고 Outlier는 큰 cov값을 갖는 점이 있을 테니 이것이 상관관계의 왜곡을 만들어 냅니다
• Outlier가 있는 경우에 Robust 하게 상관관계를 측정할 수 있는 방법이 있는데 그것이 Spearman 상관계수
• 숫자 데이터에 순위를 다시 매긴 후에 그것을 이용
• 범주형 데이터가 순서를 갖는 Ordinal 데이터라면 범주형 데이터를 raw 데이터가 아니라 순서에 맞도록 순위를 매긴후에 그 순위를 숫자와 똑같이 취급하면 또 그 나름대로의 상관관계를 따질 수 있습니다

– 연속변수라 하더라도 극단적인 값들이 존재하면 Pearson Correlation 대신 Spearman 상관계수를 사용할 수 있음.

– 계산 방법은 자료의 서열을 정한 다음, 이 서열간의 Pearson 상관계수를 계산하면 됨.

 

Spearman 상관계수는 Pearson 상관계수로부터 시작

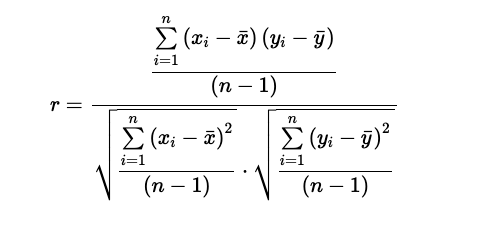
예제 하나 정도는 보고 가면 이해에 많은 도움이 되겠습니다. 방금 이야기한 직원들의 출근순서와 근속개월의 관계를 간단하게 볼까요?

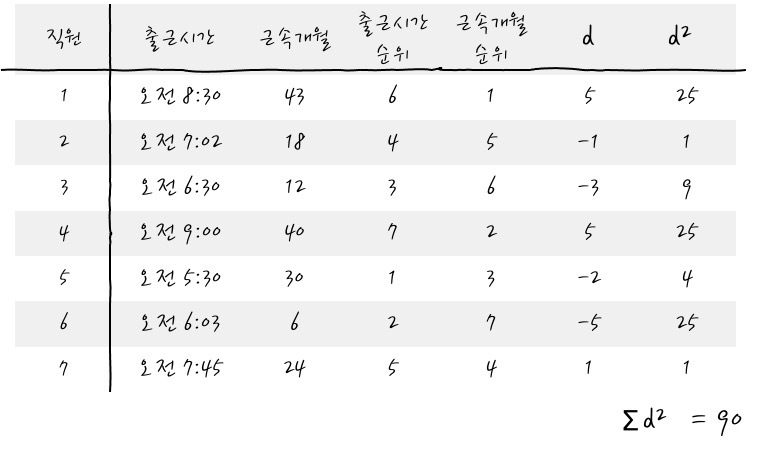
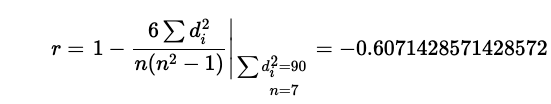
 입니다. 어, 꽤 큰 음의 상관관계가 있군요? 이렇다는 이야기는 근속기간이 길수록 순위가 작고, 출근 시간이 빠를수록 순위가 작으니까, 근속기간이 길수록 출근 시간이 늦은 것 아닌가 하는 관계를 생각해 볼 수 있겠습니다만. scipy를 이용해서 p value를 계산해 보면

from scipy.stats import spearmanr
spearmanr(df_raw['출근시간순위'], df_raw['근속개월순위'])
>
SpearmanrResult(correlation=-0.6071428571428572, pvalue=0.1482311614811614)​

엇. p value가 유의하지는 않습니다? 이 이야기는 표본에 대해서는 높은 상관관계를 보이는 것처럼 보이지만, 막상 모집단에서의 상관관계는 없다고 봐야 한다 정도로 interpretation을 하면 되지 않을까 합니다.

- 사실 이 경우는 상관관계가 크게 나옴에도 불구하고 Significant하지 않게 나온 이유는 표본의 크기가 너무 작아서라고 보는 것이 훨씬 현실적입니다. - 다행히 spearmanr과 손으로 푼 것이 같은 값이 나왔으나 표본크기가 작은 경우에는 두 결과가 다르게 나오는 경우도 있습니다. 좀 그렇죠. 이런식으로 상관관계를 보는 켄달계수라는 것도 있는데 이건 그런 게 있었나 정도로 끝내는 것이 좋겠습니다.  생각보다 너무 긴 이야기가 되어 버렸군요. 

 

---

• Phi(φ) coefficient.

– 두 범주 변수들간의 상관계수

– 각 범주 변수를 0과 1로 바꾼 다음, 이 둘 간의 Pearson 상관계수로 계산할 수 있음.

– 이 값은 부호가 의미가 없고, 최소값이 0은 아니다.

 

• Tetrachoric 상관계수

– 범주들간의 상관계수이나, 범주들이 인위적으로 이분화된 경우에 사용하는 이다.

– 이분화되기 전 원래 변수는 정규분포를 띠고 있다고 가정한다.

 

• 점이연 상관계수 (Point-biserial correlation)

– 하나가 연속변수이고 다른 하나고 이분변수일 때 사용하는 상관계수

– 이분변수를 0과 1로 코딩한 다음 Peason 상관계수를 계산하면이 상관계수가 된다.

– 검사에서 총점과 문항 (correct/incorrect 혹은 yes/no) 간의 상관계수를 구할 때 자주 사용된다.

– 두 집단의 t-검증과 밀접히 관련되어 있다.

 

• 이연 상관계수 (Biserial correlation)

– 하나가 연속변수이고 다른 하나고 이분변수일 때 사용하는 상관계수이지만 이분변수가 원래 연속변수인데 이분화한 경우에 상용한다.

– 이는 이분화되지 않았을 때 두 연속변수들간의 상관계수를 추정하는 방식으로 상관이 구해진다.

 

(출처 : http://qpsy.snu.ac.kr/teaching/multivariate/R_V.pdf) https://dohwan.tistory.com/394 )

상관계수의 종류(Point-Biserial, Biserial Correlation, etc.)